如何通过牛顿法求近似平方根？

这是一篇考拉内部小型技术分享的文章。
这次分享一个求近似平方根的快速方法: 牛顿法。
先上代码:

def sqrt(n): ret = n while ret * ret > n: ret = (ret + n / ret) / 2 return ret print(sqrt(4)) print(sqrt(2)) 

代码很简短，很神奇，为什么这样子可以求出来平方根呢？下面来推导一下。

设 n 的平方根为 x， 则有 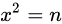, 即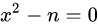, 写成对 x 的函数的形式为。假设 n=4, 我们都知道，4 的平方根是 2，那用牛顿法怎么求出来呢？先画出来这个函数的图形。

from matplotlib import pyplot as plt import numpy as np %matplotlib notebook xs = np.linspace(-6, 6, 1000) ys = [x * x - 4 for x in xs] plt.xlabel('x') plt.ylabel('y') plt.plot(xs, [0] * 1000) plt.plot([0] * 1000, np.linspace(-6, 30, 1000)) plt.plot(xs, ys) 

<IPython.core.display.Javascript object> 

[<matplotlib.lines.Line2D at 0x1217b25f8>] 

然后我们取一个点，先取点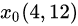, 然后做一条切线，它会跟 x 轴相交于点(2.5, 0), 相同横坐标对应函数上的点为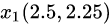, 然后我们在 x1 处再做一条切线，它会和 x 轴相交于点(2.05, 0), 相同横坐标对应函数上的点为 x2(2.05, 0.2025), 继续这样迭代下去，将很快求出来最后 x 是 2.

def f(x): return x * x - 4 xs = np.linspace(-6, 6, 1000) ys = [f(x) for x in xs] plt.xlabel('x') plt.ylabel('y') plt.plot(xs, [0] * 1000) plt.plot([0] * 1000, np.linspace(-6, 30, 1000)) plt.plot(xs, ys) plt.plot(4, f(4), 'ro') plt.annotate('x0(4, 12)', (2, 12)) plt.plot([4, 4], [0, 12], '--') k0 = (f(4 + 0.1) - f(4 - 0.1)) / 0.2 b0 = f(4) - k0 * 4 def f_tangent0(x): """ 点 x0 的切线方程 """ return k0 * x + b0 xs = np.linspace(2, 6, 1000) ys = [f_tangent0(x) for x in xs] plt.plot(xs, ys) plt.plot(2.5, f(2.5), 'ro') plt.annotate('x1(2.5, 2.25)', (0.5, 5)) plt.plot([2.5, 2.5], [0, 2.25], '--') k1 = (f(2.5 + 0.1) - f(2.5 - 0.1)) / 0.2 b1 = f(2.5) - k1 * 2.5 def f_tangent1(x): """ 点 x1 的切线方程 """ return k1 * x + b1 xs = np.linspace(1, 6, 1000) ys = [f_tangent1(x) for x in xs] plt.plot(xs, ys) # plt.plot(2.05, f(2.05), 'ro') # plt.annotate('x1(2.05, 0.2)', (2.05, -5)) 

<IPython.core.display.Javascript object> 

[<matplotlib.lines.Line2D at 0x12ee97c18>] 

从图形上可以比较直观的理解牛顿迭代法，但是从代数上怎么进行计算呢？现在来推导一下:

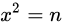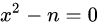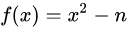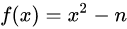设 n 的平方根为 x， 则有 , 即, 写成对 x 的函数的形式为，我们取一个点, 作一条切线，那么切线的斜率 k 就是的导数:

由上面的图可以看出来，作 x0 到 x 轴的垂线，围成了一个三角形，由三角定理可知:

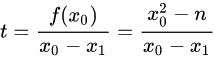
所以有:

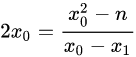
化简得:

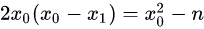
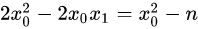
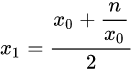
再看一次代码:

def sqrt(n): ret = n while ret * ret > n: ret = (ret + n / ret) / 2 return ret 

一致!

牛顿迭代法求平方根就是这样推导出来的。

其实牛顿法，除了应用在求平方根上，还有很多应用，在机器学习算法的最后优化步骤中，会使用牛顿法求任意函数的最优解，不仅限于这种类型。

建议大家做一下 leetcode 这道题: sqrtx，会加深理解。

分享内容出自考拉程序猿 Hank 的 blog Hank ‘ s blog