这是一个专门讨论 idea 的地方。
每个人的时间,资源是有限的,有的时候你或许能够想到很多 idea,但是由于现实的限制,却并不是所有的 idea 都能够成为现实。
那这个时候,不妨可以把那些 idea 分享出来,启发别人。
每个人的时间,资源是有限的,有的时候你或许能够想到很多 idea,但是由于现实的限制,却并不是所有的 idea 都能够成为现实。
那这个时候,不妨可以把那些 idea 分享出来,启发别人。
这是一个创建于 2835 天前的主题,其中的信息可能已经有所发展或是发生改变。
这一数值本身是在 2017 年 12 月 26 日被发现的。检验又花费了六天的功夫,进行不间断的计算。接下来,又在四种不同的硬件配置上,运行了四个不同的程序来进一步确认。
之前的记录是 2016 年 1 月发现的 M74207281,比 M77232917 少 910807 位。
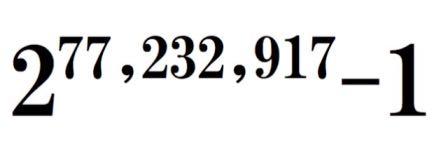
1 chanssl 2018-01-07 20:16:03 +08:00 明明是第 50 个 |
2 h4lbhg1G 2018-01-07 20:18:53 +08:00 好了我来玩坏一下热心网友,打印出来有多长 |
3 codeeer OP 哈哈哈哈哈多谢提醒,这是第 50 位! |
6 outloudvi 2018-01-07 21:01:32 +08:00 via Android 呃……咕咕机…… |
7 zthxxx 2018-01-07 21:17:16 +08:00 len(str(2**77232917)) 位 |
8 rogwan 2018-01-07 21:23:31 +08:00 梅森素数很矫情,迄今才发现了区区 50 个,却不知道是否有无穷多个,哎 。。。 |
9 ob 2018-01-07 21:26:54 +08:00 via Android 吓得我赶紧查下百科看是什么东西 |
12 xiaosaiyin 2018-01-07 23:20:27 +08:00 In[1]:= N[Log[10, 2^77232917 - 1]] Out[1]= 2.32494*10^7 |
13 ZhaoMiing 2018-01-08 00:12:21 +08:00 学渣问一句找它有啥意义(瑟瑟发抖 |
14 YyYyYyy 2018-01-08 01:05:48 +08:00 @ZhaoMiing 据我这个学渣的浅薄知识,鉴于最近捣鼓 C++库看见过梅森旋转,这个素数可能和快速产生高质量的伪随机数有关? |
15 artandlol 2018-01-08 01:38:58 +08:00 2^(素数)-1 这类超级计算机应该都算过,最后怎么是个人找到的呢? 个人才花了 6 天,超算也就几个小时吧 |
16 sneezry 2018-01-08 01:47:46 +08:00 |
17 h4lbhg1G 2018-01-08 01:52:44 +08:00 @artandlol 是个人么?看上去是和那个众包产生 1000 甚至 1 千万作者的论文一个路子吧。质数对于计算机应该是难题啊,哪会这么容易解决,目前互联网安全的基石 SSL 也才 2048 位二进制的 RSA 素数而已啊。 |
19 WindowPain 2018-01-08 02:05:26 +08:00 第一次知道梅森素数还是 7 年前,转眼又发现了 4 个了…… |
20 wallriding 2018-01-08 02:47:58 +08:00 这个数是素数要怎么验证呢?跟平常用的判断素数方法一样吗?哪位大佬说一下? |
21 quinoa42 2018-01-08 04:38:05 +08:00 |
22 InfinityJK 2018-01-08 16:28:23 +08:00 打印出来大概要高精度乘,用 fft 一次乘法 nlogn,n 是位数,快速幂 lgn,n 是幂大小,emmm 普通计算机可能要跑 1s? 不知道算的对不对 |
23 allen666 2018-01-18 09:45:11 +08:00 Prime95 就是算这玩意的,以前拷机算了不少啊,算是做了贡献了 |
